Towards Empirical Robustness
in Network Epistemology

Max Noichl, Ignacio Quintana & Hein Duijf

2024-10-25

https://tinyurl.com/2r72fbm9

Outline

  • Intro: Network epistemology
  • Robustness
  • How to align empirical and simulated networks?
  • Some results
  • Work in progress!

Network epistemology

  • Traditional epistemology focuses on individual rationality
    • What is the proper response to evidence?
  • Network epistemology can target the structure of communication
    • Which communication structures are best?
  • First main results by Kevin J. S. Zollman (2007) who uses agent-based modelling and simulations

Recap: Zollman (2007, 2010)

  • Agents (scientists) evaluate two competing methods, with similar, but slightly different quality. (Bandit-problem mirroring clinical trials). They communicate their evidence on a network.
  • Agents cease evaluating methods they believe to be inferior.
  • Main findings:
    • Less connectivity can lead to more reliable groups – Community structure matters!
    • There is a trade-off between speed of convergence and reliability

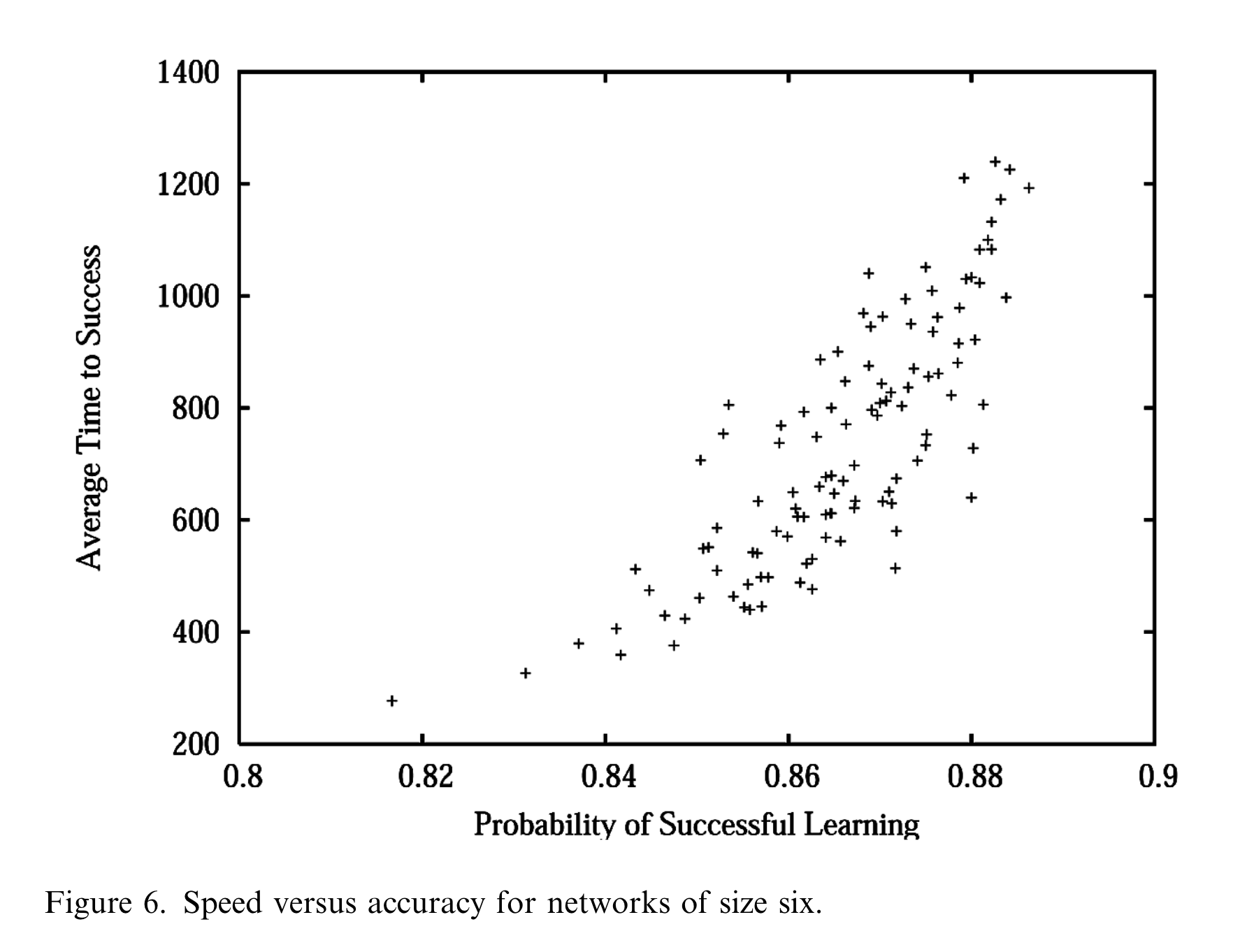
Accuracy vs. Speed – Kevin J. S. Zollman (2007)

“Even beyond the problem of maintaining the division of cognitive labor, this model suggests that in some circumstances there is an unintended benefit from scientists being uninformed about experimental results in their field. This is not universally beneficial, however.

In circumstances where speed is very important or where we think that our initial estimates are likely very close to the truth, connected groups of scientist will be more reliable. On the other hand, when we want accuracy above all else, we should prefer communities made up of more isolated individuals.” – Kevin J. S. Zollman (2007)

Following these strands in Network Epistemology

  • A strand on robustness:
    • Robustness under changes in parameter settings (Rosenstock, Bruner, and O’Connor (2017)),
    • Robustness under changes in modelling choices (Kummerfeld and Zollman (2016); Frey and Šešelja (2018a); Frey and Šešelja (2020); Frey and Šešelja (2018b); Jonard, Reijula, and Marengo (2024))
  • A strand on conformity: (Kevin James Spears Zollman (2010); Mohseni and Williams (2021); Weatherall and O’Connor (2021); Fazelpour and Steel (2022))
  • A strand on epistemically impure agents (including financial interests) (Holman and Bruner (2015); Weatherall, O’Connor, and Bruner (2020))
  • Our work: Empirically guided robustness tests.

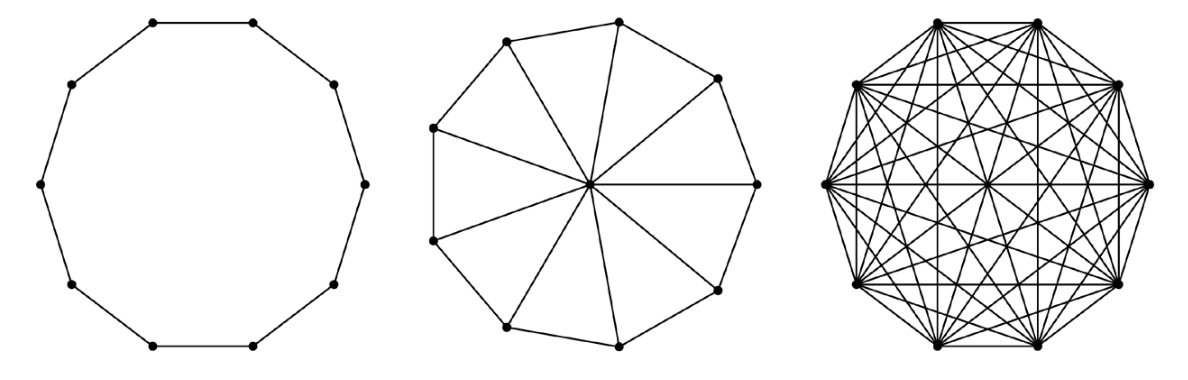
Main network-types used in Kevin J. S. Zollman (2007)

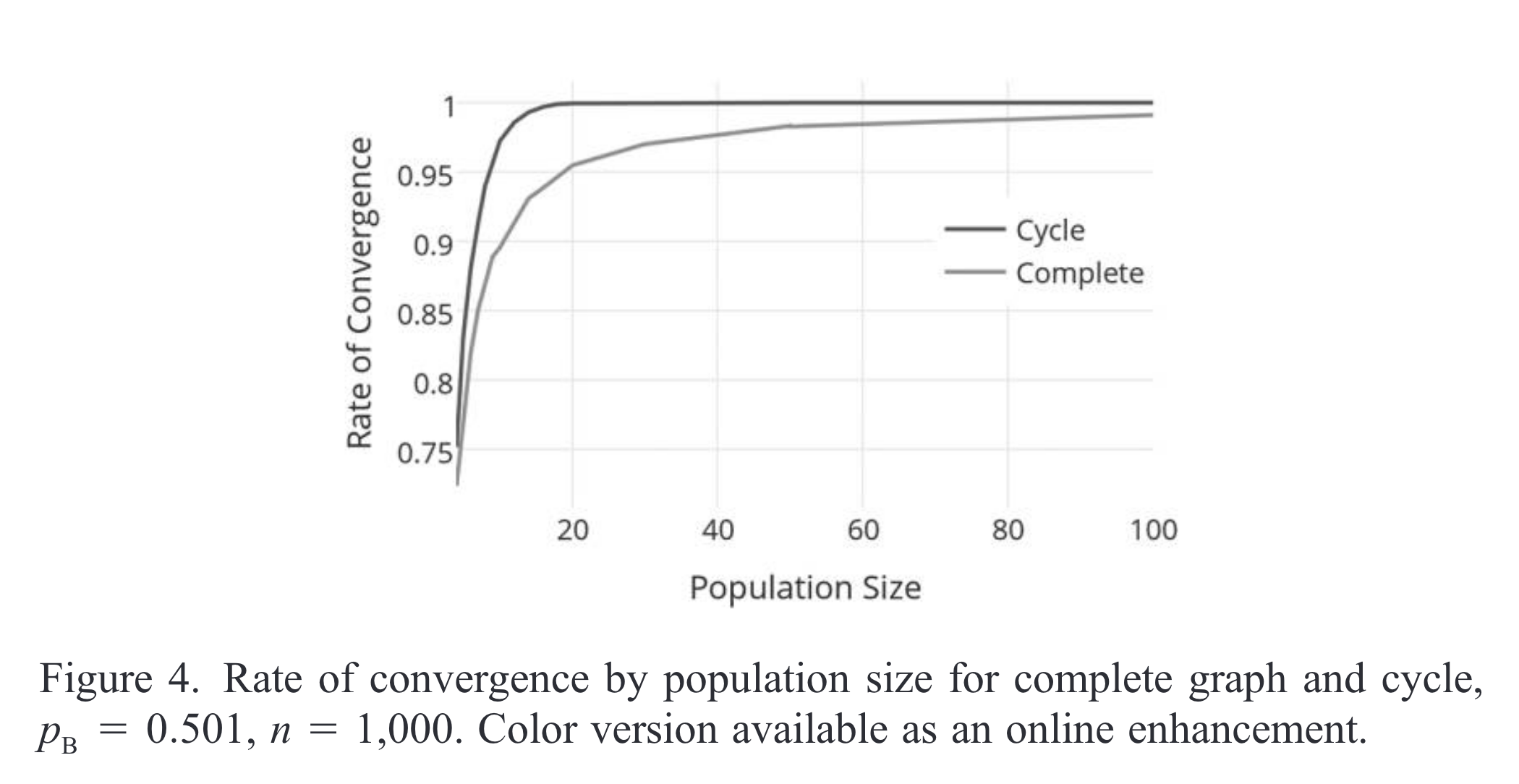
Convergence as a function of network-size – Rosenstock, Bruner, and O’Connor (2017)

“As a result, we cannot say with confidence that we expect real world epistemic communities to generally fall under the area of parameter space where the Zollman effect occurs. We are unsure whether they correspond to this area of parameter space, or some other area, or some other models with different assumptions.” – Rosenstock, Bruner, and O’Connor (2017)

But we care about

real world

epistemic communities!

How to choose networks?

  • There are many potentially relevant generative network-models.
  • All have associated parameter spaces.
  • We need to find which ones fit the networks that we are actually interested in.
  • Idea: Gather some empirical networks, and try to get our candidate models to reproduce them.

Step 1: Empirical networks

  • There are several examples of sub-optimal processes in the history of science.
  • “The hypothesis that peptic ulcers are caused by bacteria did not originate with Warren and Marshall, it predates their births by more than 60 years. But, unlike other famous cases of anticipation, this theory was the subject of significant scientific scrutiny during that time. To those who have faith in the scientific enterprise, it should come as a surprise that the widespread acceptance of a now well supported theory should take so long.” – Kevin J. S. Zollman (2010)
  • Our current Examples: Peptic Ulcer (n= 2360, – 1978) & Perceptron (n= 943, – 1979)
  • Author based citation-network collected from OpenAlex, identical agents merged, undirected(!).

the perceptron network















Step 2: Try to fit candidate models

  • Using an optimization-framework borrowed from ML, hyperopt, we try to find the parameters that produce networks similar to the ones we are interested in.
  • Similarity is defined as the MSE between the standardized network-statistics of the generated network and the empirical network.
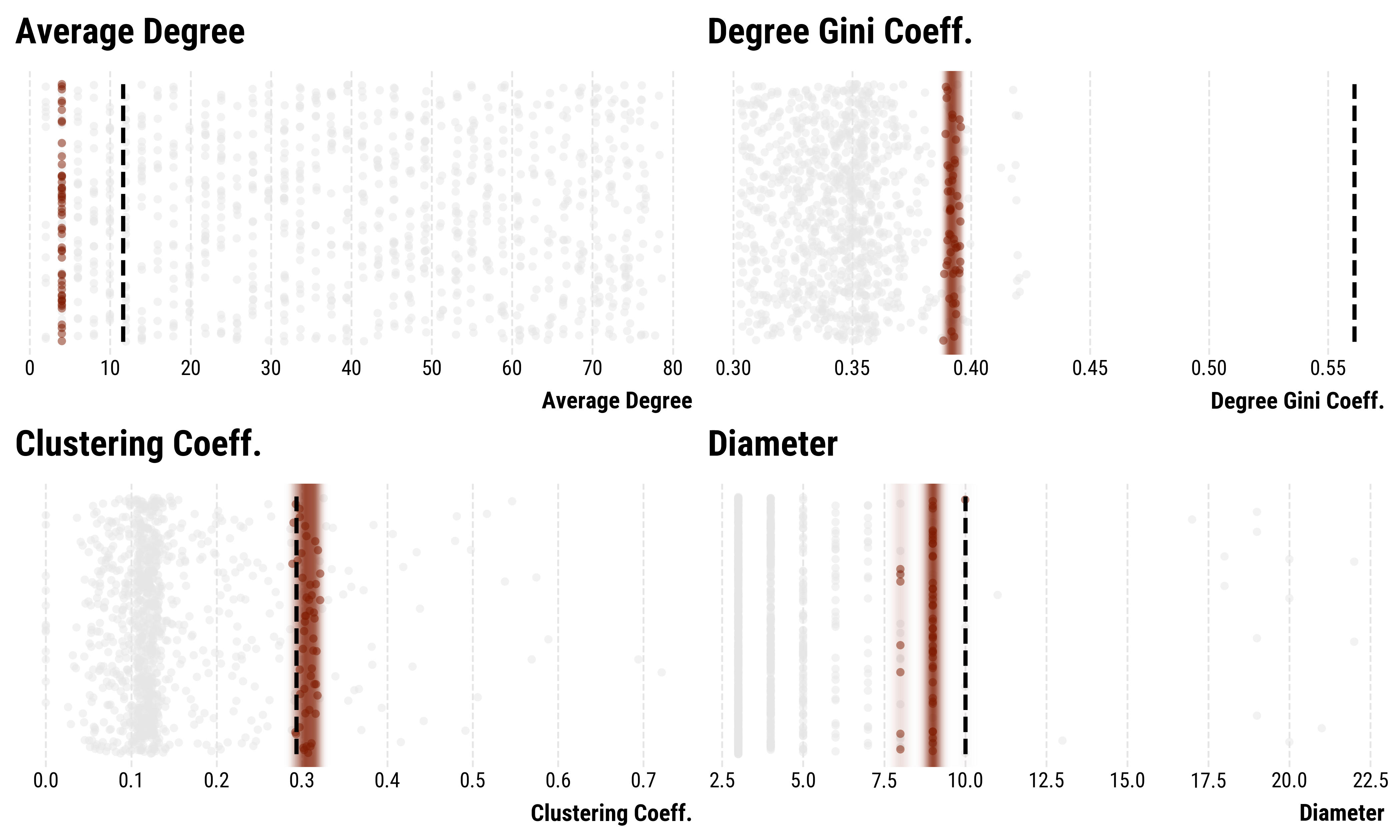
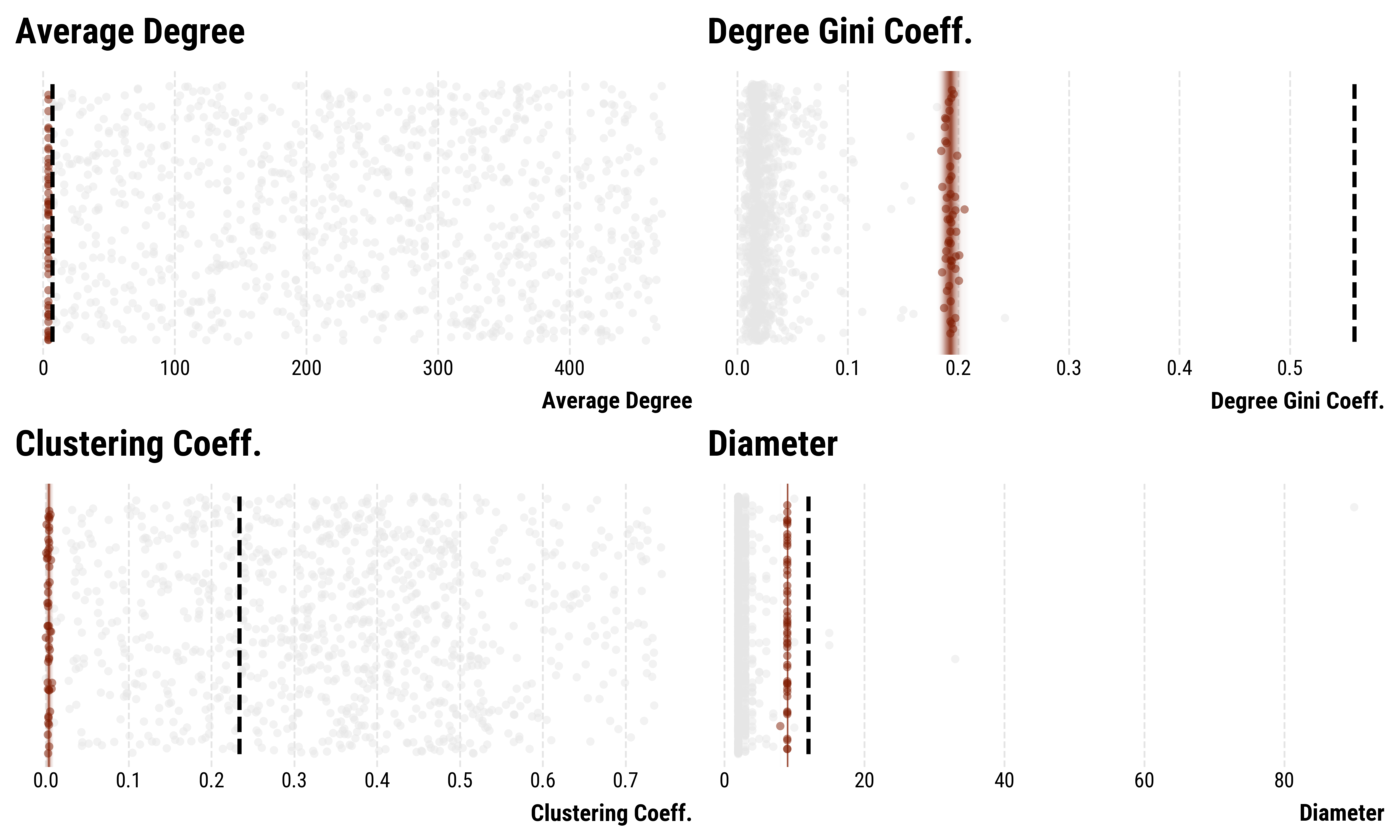
  • We focus on the degree heterogeneity (Gini-coefficient), average clustering-coefficient, diameter and average degree.

Parzen tree optimization: Example

  • We try to fit a Holme-Kim model to an artificially generated one with parameters m=12, p=0.22.
    • Explanation after Horgan (2023)
  • First we generate 50 random samples from the parameter space…

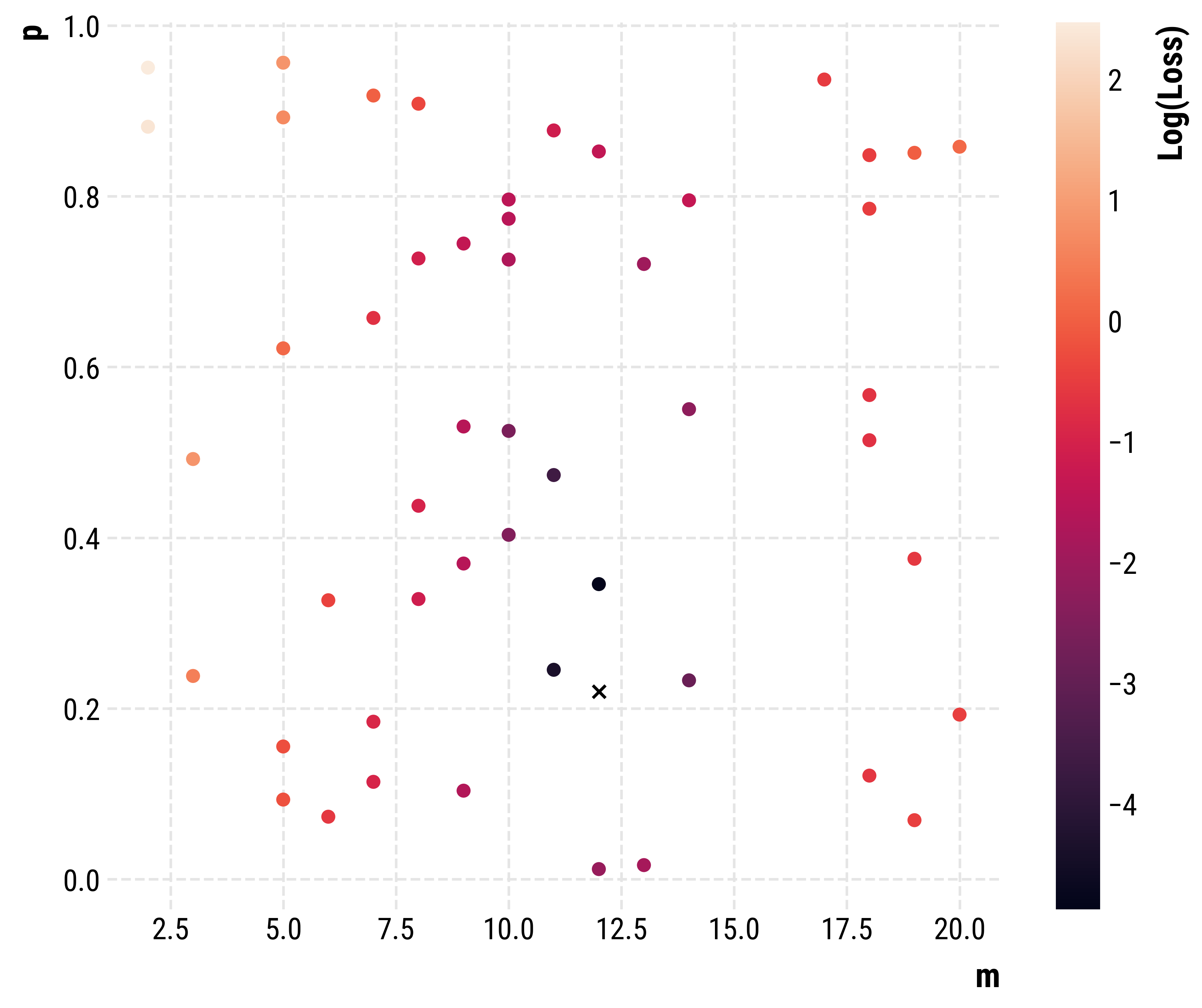
50 initial samples from the parameter space. The cross marks the true parameters.

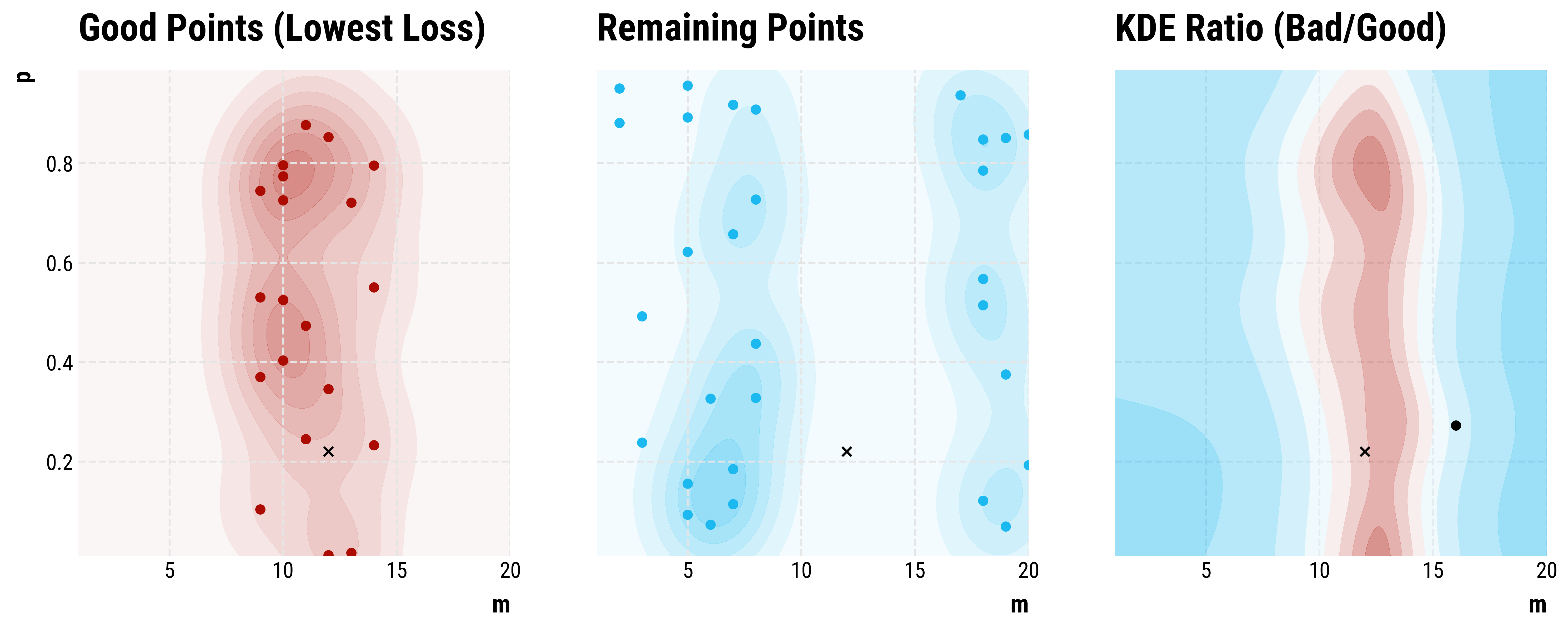
Step 50: We then choose the top \(\gamma\) of samples, and calculate a density estimate for their region \(l(x)\), as well as the remainder, \(g(x)\). We randomly sample points, and chose the point that maximizes \(g(x) / l(x)\).

Step 75: We repeat the process, now using the new samples…

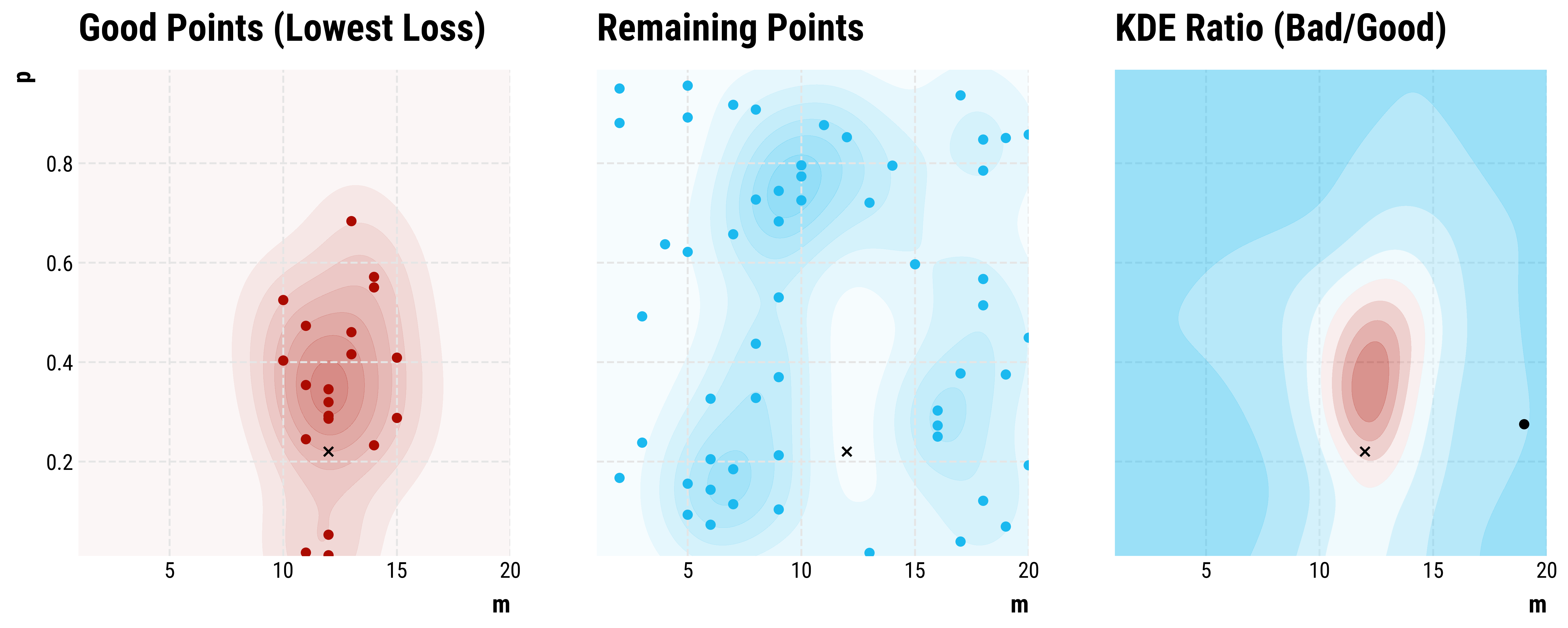
Step 125: …

Step 150: …

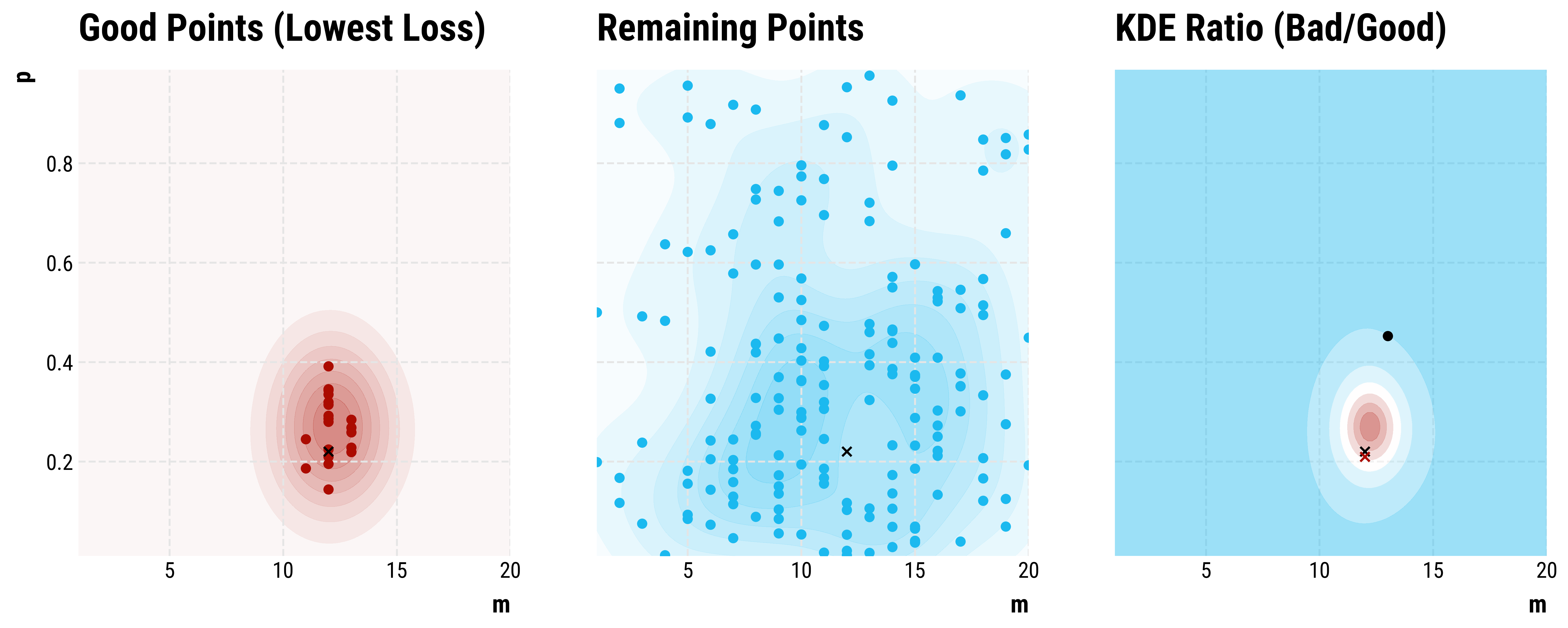
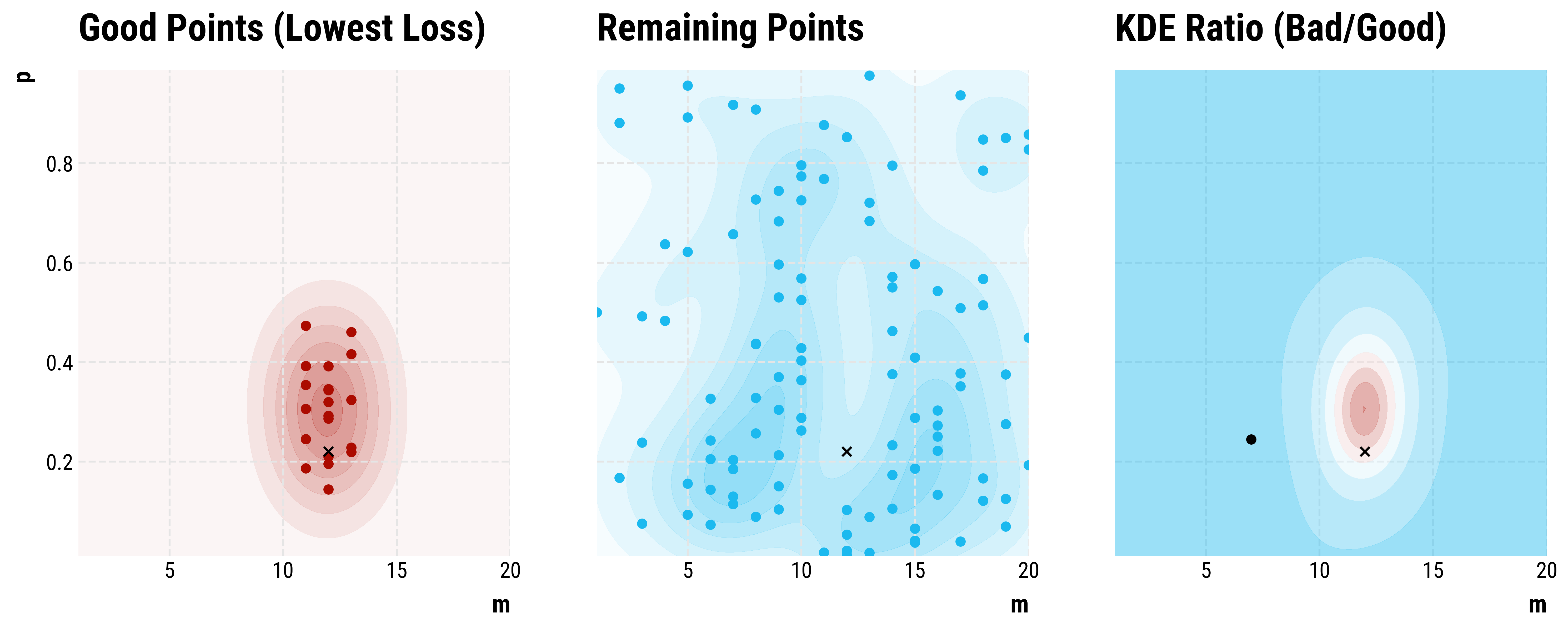
Step 198: …

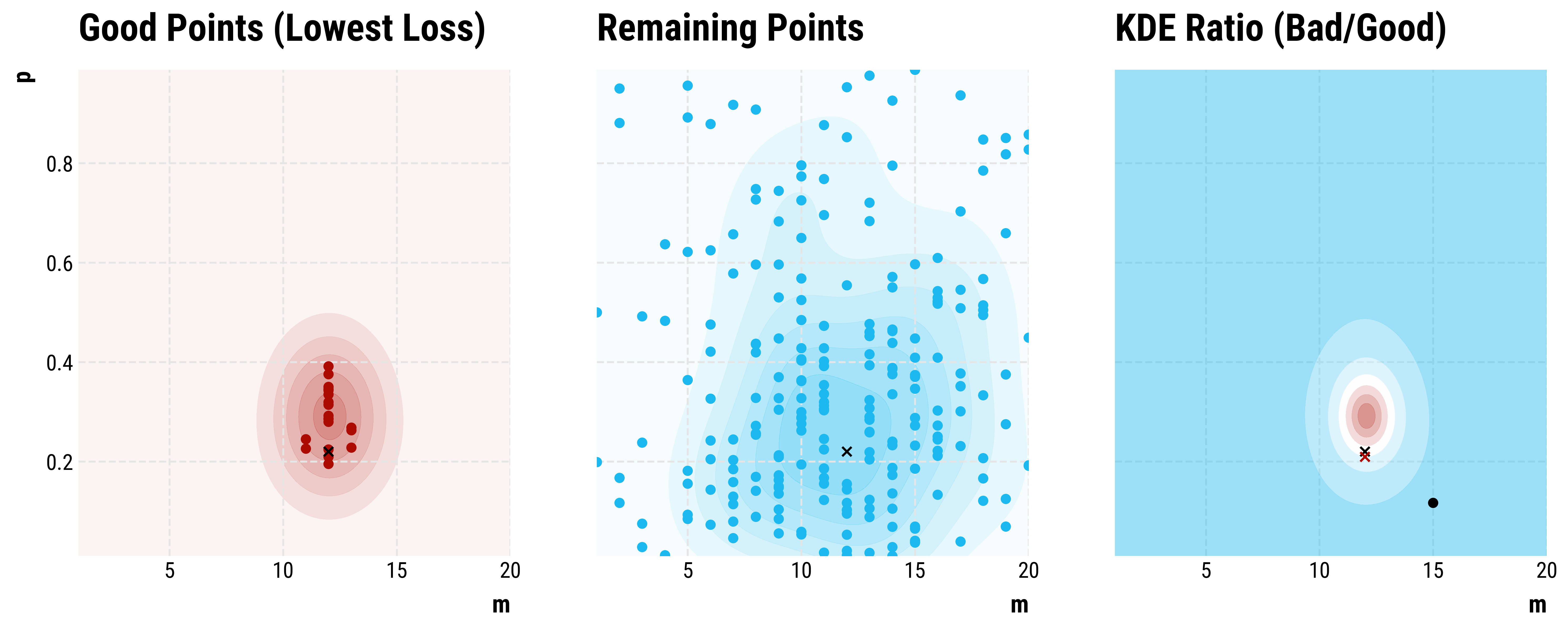
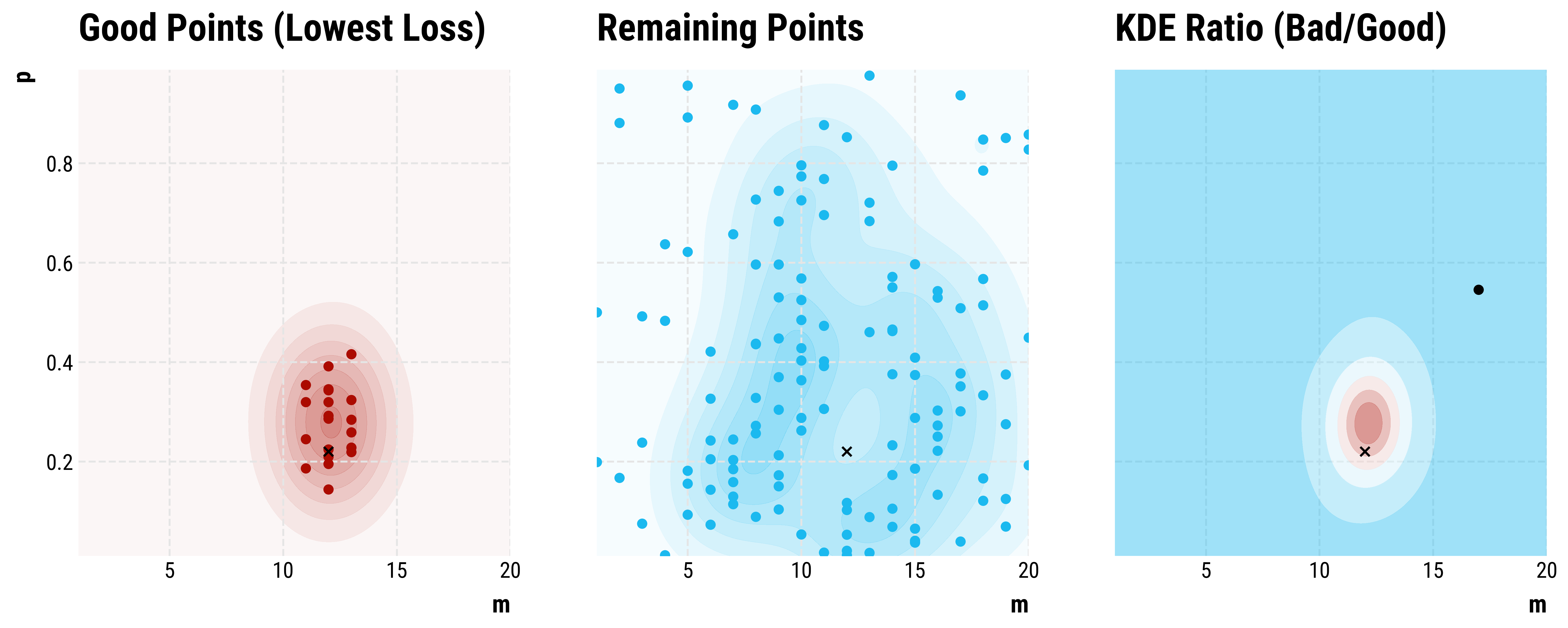
Step 248: The optimization is complete. We recovered \(m ≈ 12, p ≈ 0.26\).

Now we apply this to the

real world networks…

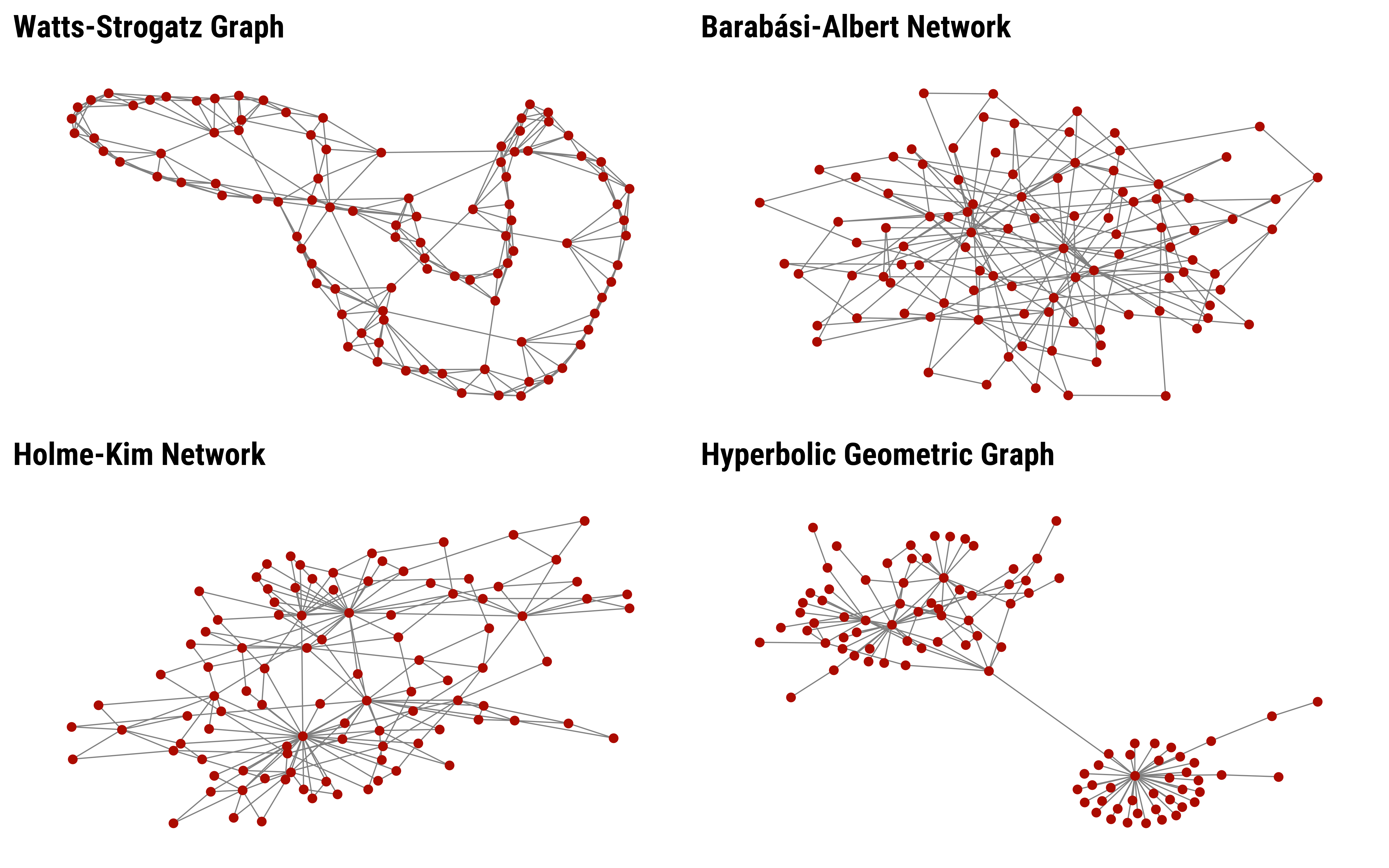
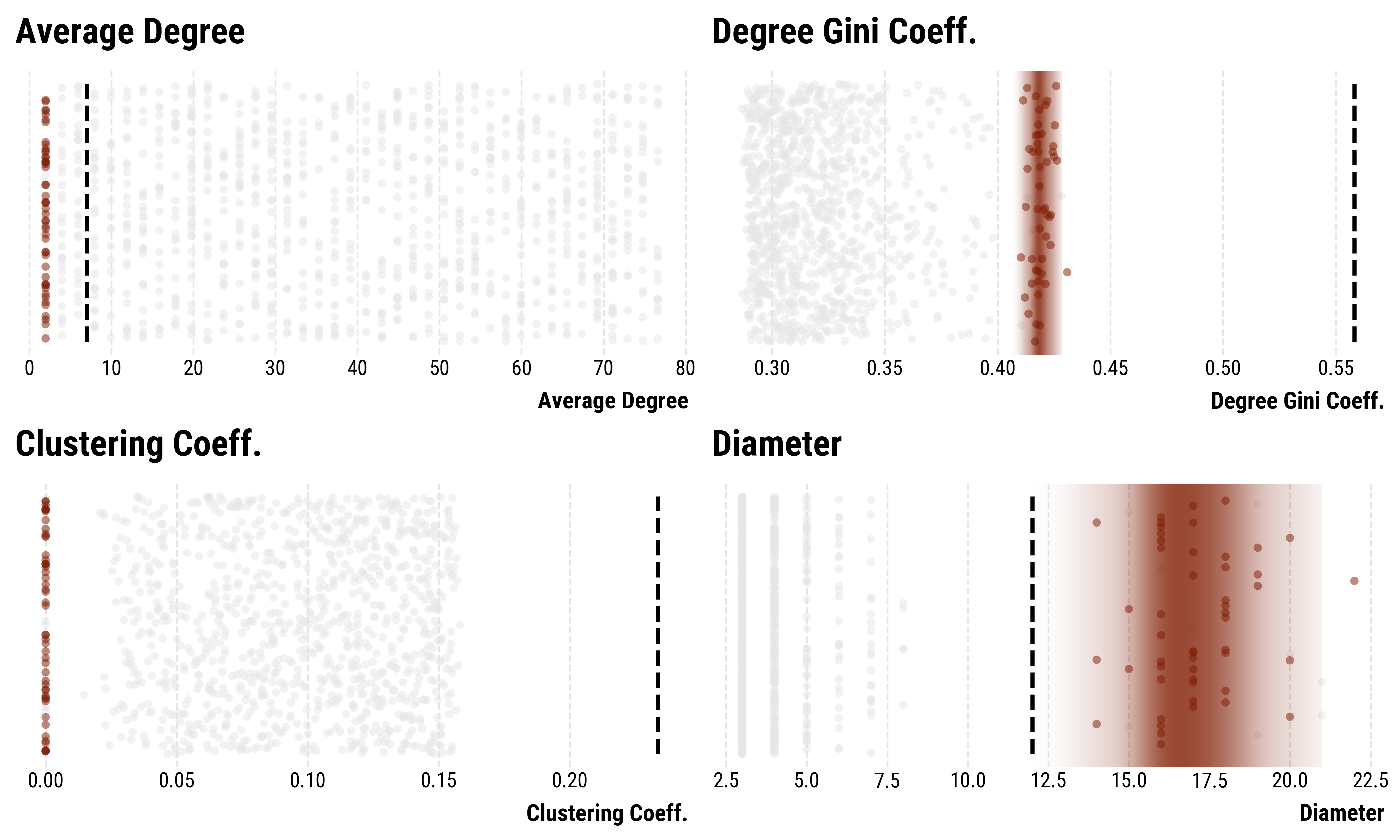
Attempt 1: Barabási-Albert model on the perceptron-network. The best recovered parameters (red) fit the empirical network (black line) very badly.

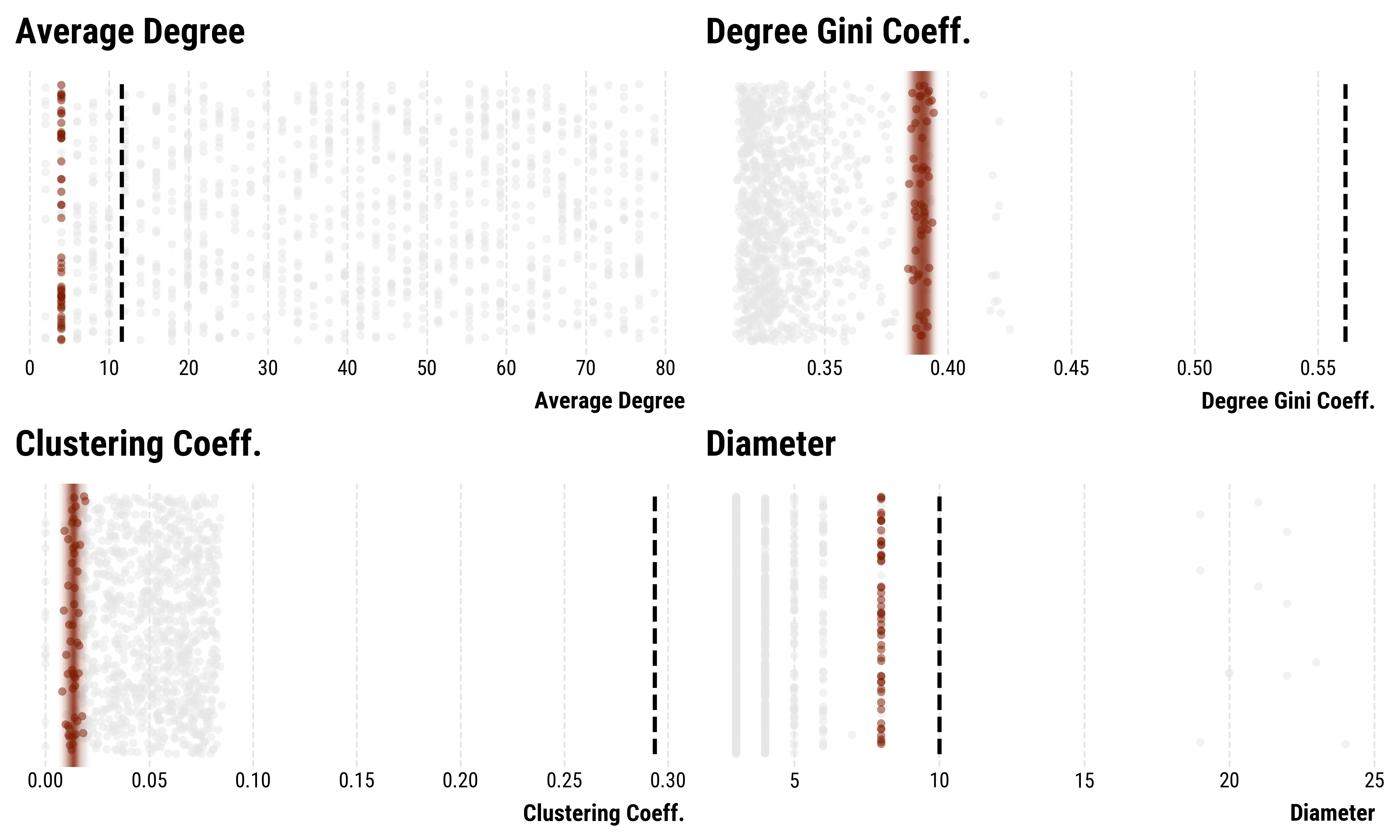
Attempt 1: Barabási-Albert model on the peptic ulcer-network.

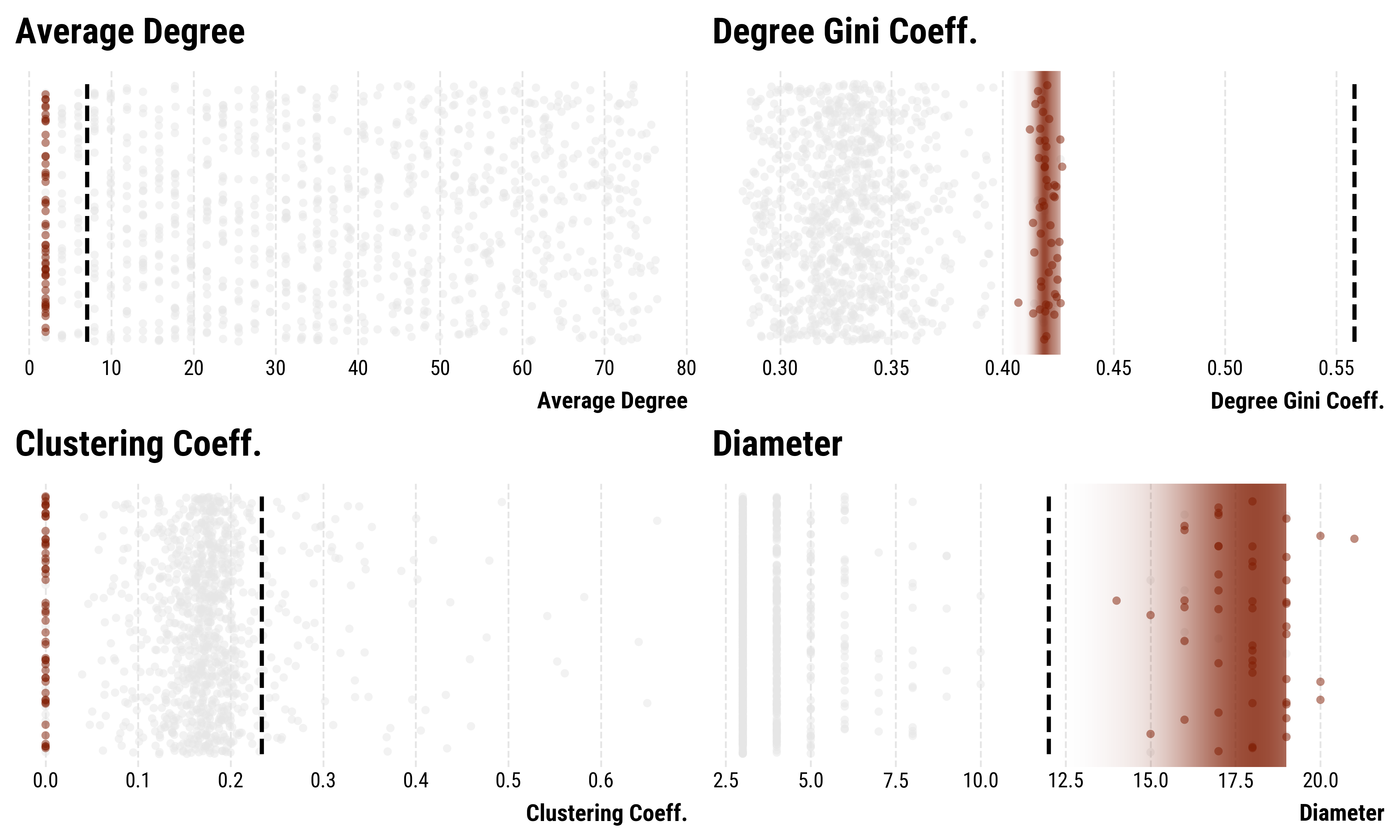
Attempt 2: Holme-Kim model on the perceptron-network.

Attempt 2: Holme-Kim model on the peptic ulcer-network.

Attempt 3: Watts-Strogatz model on the perceptron-network.

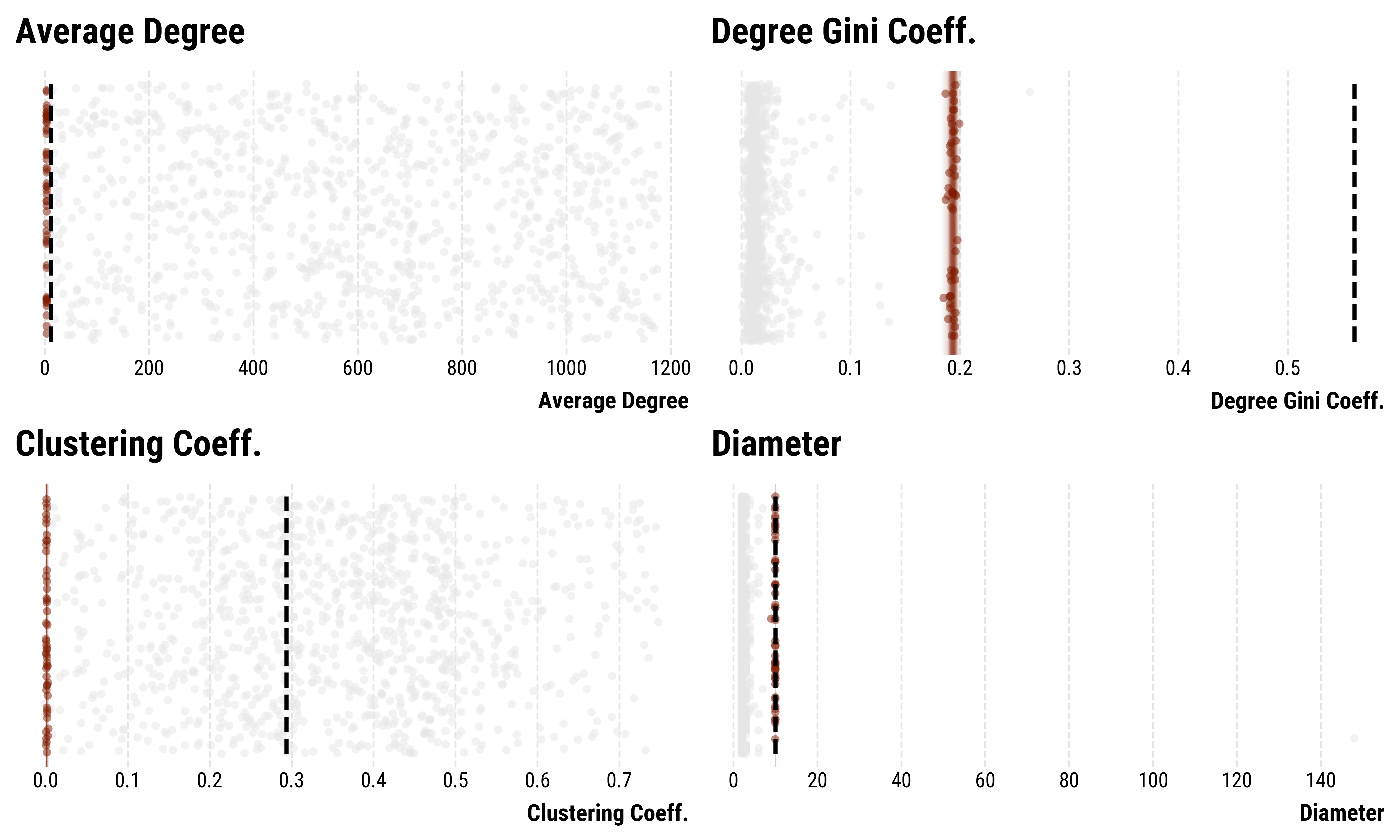
Attempt 3: Watts-Strogatz model on the peptic ulcer-network.

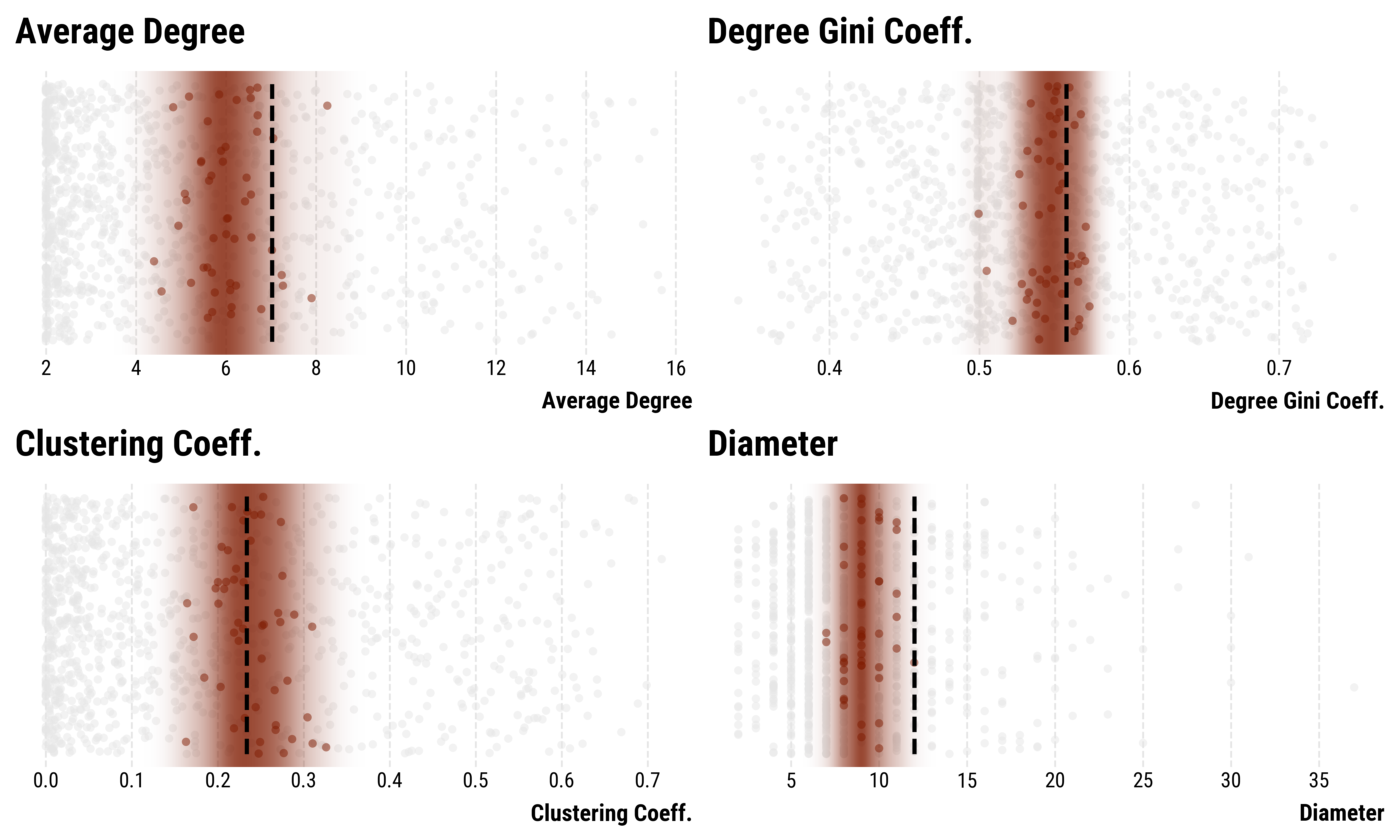
Attempt 4: Hyperbolic geometric graph model on the perceptron-network – reasonably good fit.

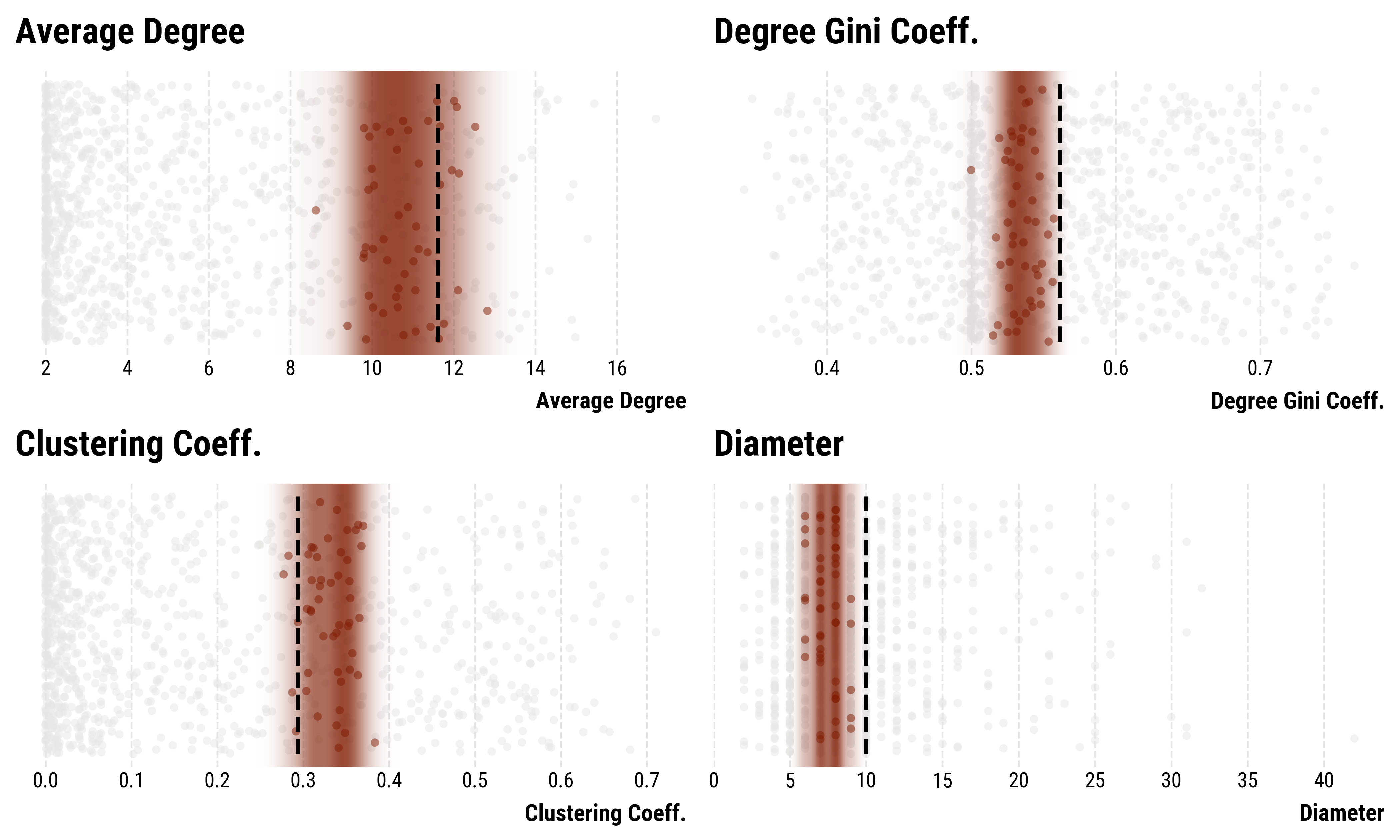
Attempt 4: Hyperbolic random geometric graph model on the peptic ulcer-network.

Summary

  • Hyperbolic geometric graph models appear to be the best fit for the empirical networks under consideration.
  • Let’s simulate!

Running the simulations

  • We run simulations on 8000 random draws from the parameter space of the hyperbolic geometric graph model, as well as 1000 simulations each on the original empirical networks.
  • We vary the easiness of the problem (how similarly good the two methods are) and the number of experiments agents can conduct each round. Agents learn via updating beta-distributions, as in Kevin J. S. Zollman (2010).
  • We keep the same network-statistics as earlier as predictive variables.
  • We focus on two outcomes:
    • The share of agents with correct knowledge at convergence.
    • The time it takes for the simulations to converge.

Results

Correctness

Share of agents with correct knowledge at convergence. Red dots indicate the empirical networks.

Speed

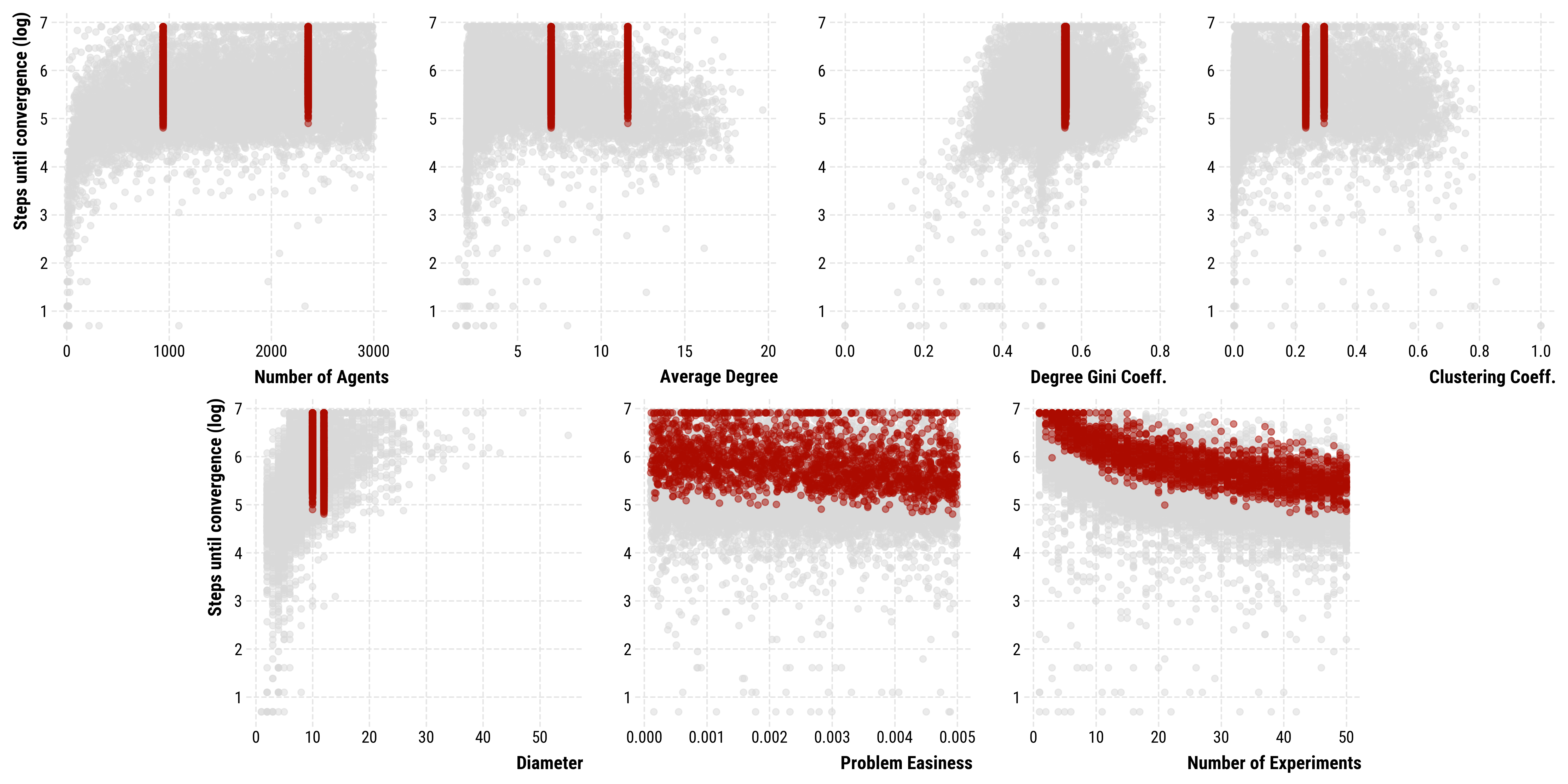
Simulation steps it takes for the simulations to converge. Red dots indicate the empirical networks.

Correctness vs Speed

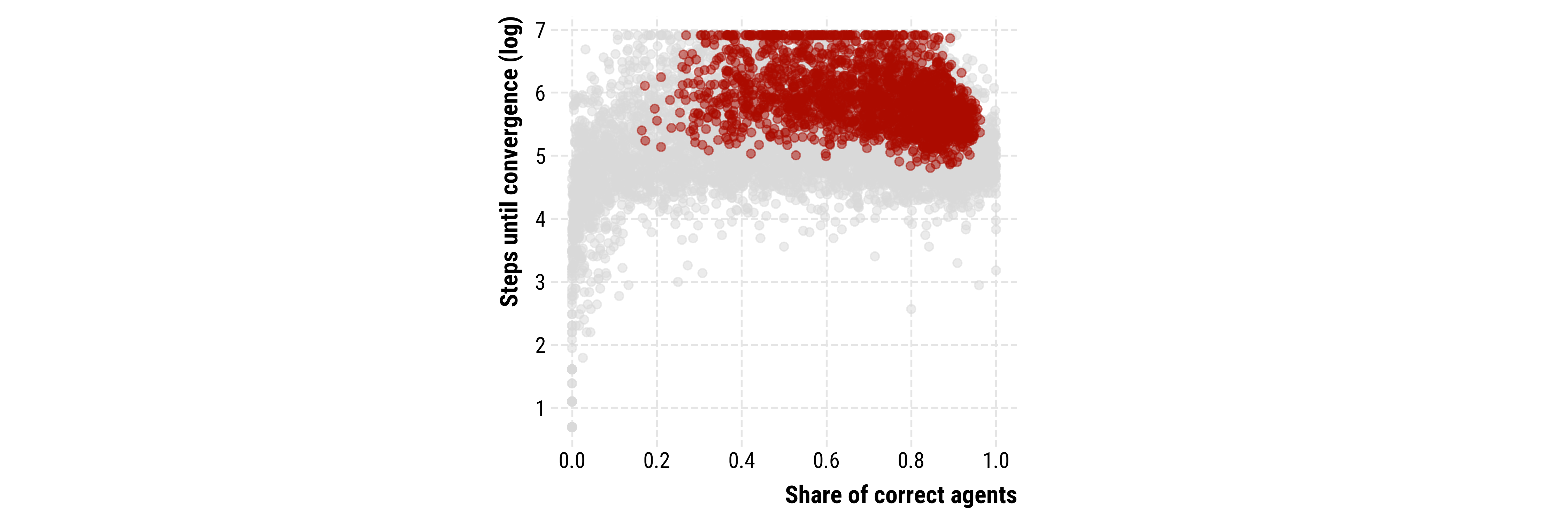
Share of agents with correct knowledge at convergence vs. simulation steps it takes for the simulations to converge. Red dots indicate the empirical networks.

Analyzing the results

  • Analyzing the results is tricky: We expect non-linear relationships, heteroscedasticity and multicollinearity between the network-statistics.
  • One approach: Train a machine learning model (XGBoost) to predict the outcomes of simulations, then use Shapley values to analyze the model.
  • Shapley values decompose the predictions into contributions of individual variables.

Analysis: Correctness

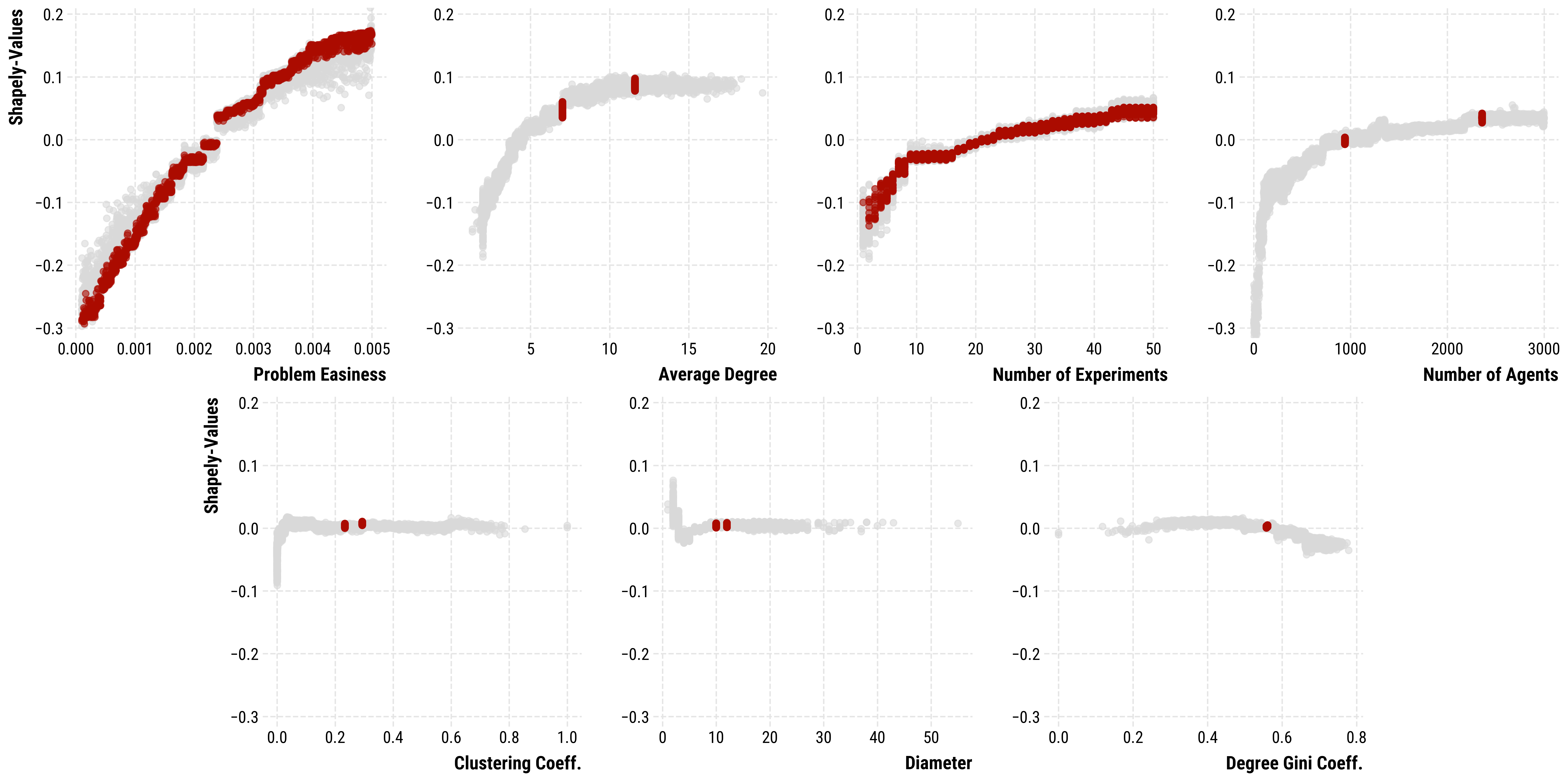
Shapley values for the XGboost model predicting the speed of convergence. Higher values indicate a higher share of agents with correct estimations.

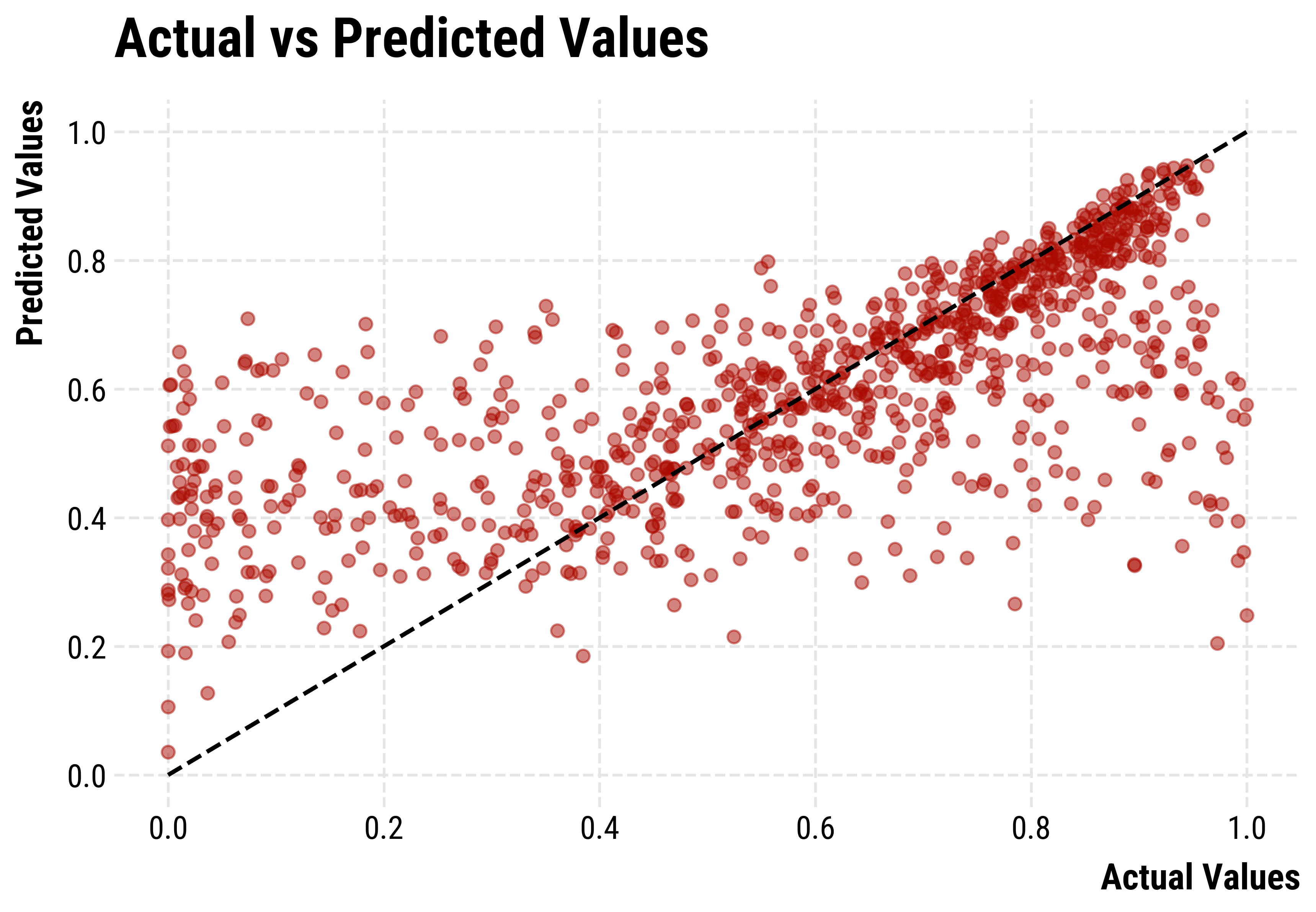
Performance of the XGBoost model predicting the share of agents with correct knowledge at convergence.

Analysis: Speed

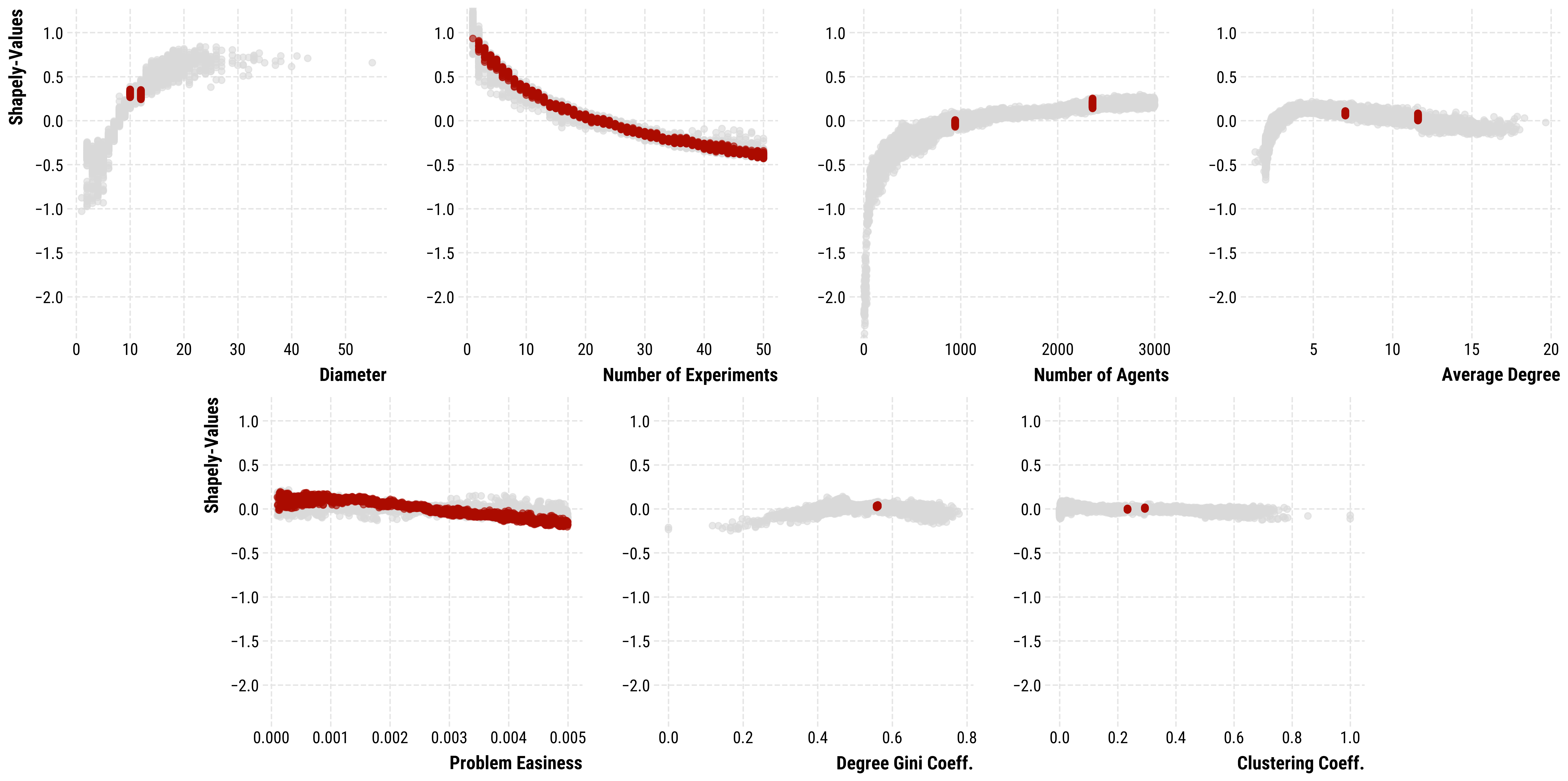
Shapley values for the XGboost model predicting the speed of convergence. Lower values indicate that variable predicts faster convergence in that range.

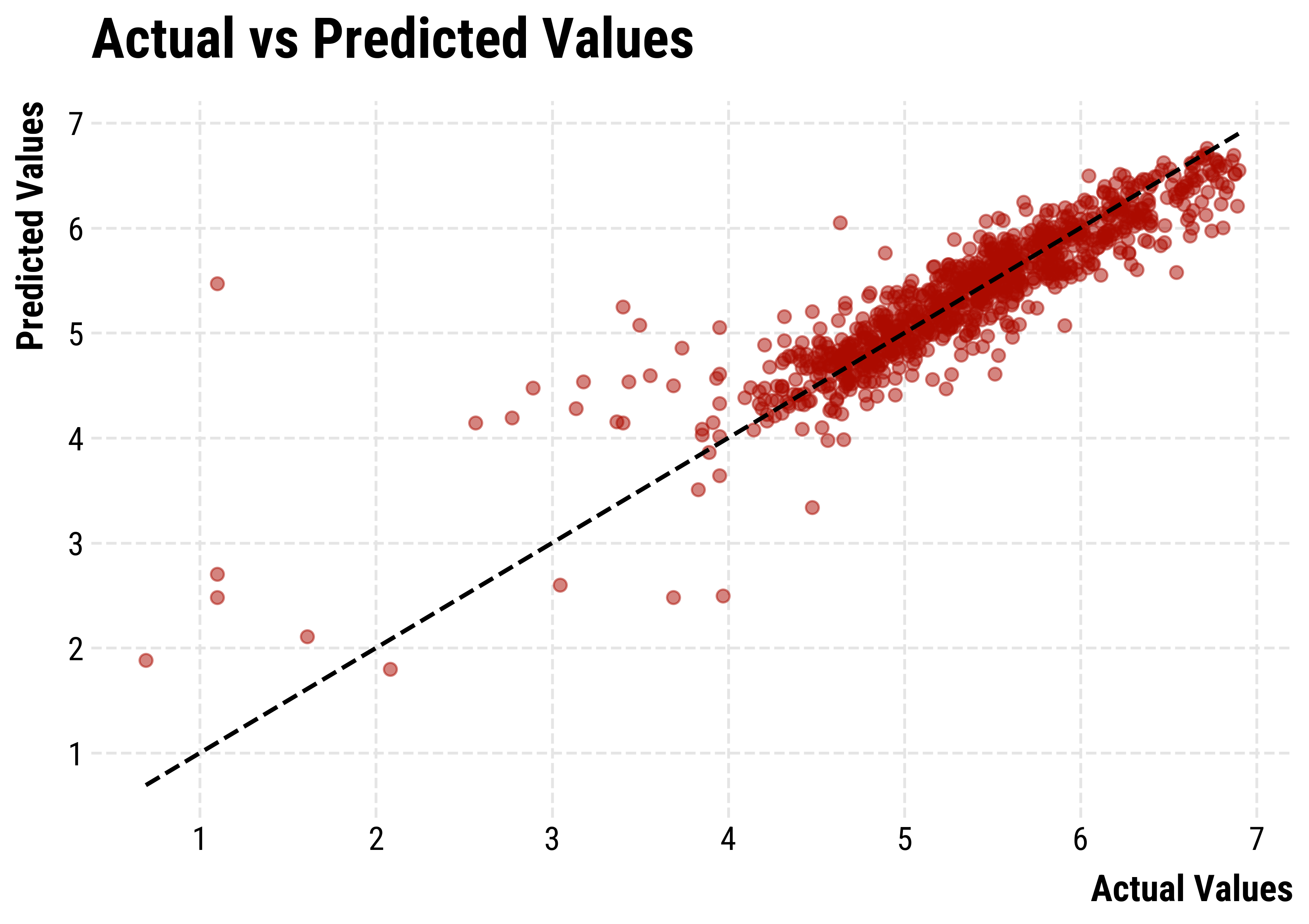
Performance of the XGBoost model predicting the speed of convergence.

Summary

  • Network properties and size matter!
  • In realistic networks, the story about speed and epistemic quality trade-offs is complicated.
  • Degree heterogeneity surprisingly doesn’t seem to matter much.

Discussion

  • What changes once we include directedness? E.g. about the influence of degree-inequality?
  • More, and more diverse case studies!
  • Additional network models?

Thank you!

Literature

Fazelpour, Sina, and Daniel Steel. 2022. “Diversity, Trust, and Conformity: A Simulation Study.” Philosophy of Science 89 (2): 209–31. https://doi.org/10.1017/psa.2021.25.
Frey, Daniel, and Dunja Šešelja. 2018b. “What Is the Epistemic Function of Highly Idealized Agent-Based Models of Scientific Inquiry?” Philosophy of the Social Sciences 48 (4): 407–33. https://doi.org/10.1177/0048393118767085.
———. 2018a. “What Is the Epistemic Function of Highly Idealized Agent-Based Models of Scientific Inquiry?” Philosophy of the Social Sciences 48 (4): 407–33. https://doi.org/10.1177/0048393118767085.
———. 2020. “Robustness and Idealizations in Agent-Based Models of Scientific Interaction.” The British Journal for the Philosophy of Science 71 (4): 1411–37. https://doi.org/10.1093/bjps/axy039.
Holman, Bennett, and Justin P. Bruner. 2015. “The Problem of Intransigently Biased Agents.” Philosophy of Science 82 (5): 956–68.
Horgan, Colin. 2023. “Building a Tree-Structured Parzen Estimator from Scratch (Kind Of).” Medium. https://towardsdatascience.com/building-a-tree-structured-parzen-estimator-from-scratch-kind-of-20ed31770478.
Jonard, Nicolas, Samuli Reijula, and Luigi Marengo. 2024. “Group Problem Solving: Diversity Versus Diffusion.” https://doi.org/10.31234/osf.io/35w76.
Kummerfeld, Erich, and Kevin J. S. Zollman. 2016. “Conservatism and the Scientific State of Nature.” The British Journal for the Philosophy of Science 67 (4): 1057–76. https://doi.org/10.1093/bjps/axv013.
Mohseni, Aydin, and Cole Randall Williams. 2021. “Truth and Conformity on Networks.” Erkenntnis 86 (6): 1509–30. https://doi.org/10.1007/s10670-019-00167-6.
Rosenstock, Sarita, Justin Bruner, and Cailin O’Connor. 2017. “In Epistemic Networks, Is Less Really More?” Philosophy of Science 84 (2): 234–52. https://doi.org/10.1086/690717.
Weatherall, James Owen, and Cailin O’Connor. 2021. “Conformity in Scientific Networks.” Synthese 198 (8): 7257–78. https://doi.org/10.1007/s11229-019-02520-2.
Weatherall, James Owen, Cailin O’Connor, and Justin P. Bruner. 2020. “How to Beat Science and Influence People: Policymakers and Propaganda in Epistemic Networks.” The British Journal for the Philosophy of Science 71 (4): 1157–86. https://doi.org/10.1093/bjps/axy062.
Zollman, Kevin J. S. 2007. “The Communication Structure of Epistemic Communities.” Philosophy of Science 74 (5): 574–87. https://doi.org/10.1086/525605.
———. 2010. “The Epistemic Benefit of Transient Diversity.” Erkenntnis 72 (1): 17–35. https://doi.org/10.1007/s10670-009-9194-6.
Zollman, Kevin James Spears. 2010. “Social Structure and the Effects of Conformity.” Synthese 172 (3): 317–40. https://doi.org/10.1007/s11229-008-9393-8.